[Paper Review] Probabilistic Symmetry and Invariant Neural Networks

1. The paper

2. Lecture by author (98) Benjamin Bloem-Reddy: Probabilistic Symmetry and Invariant Neural Networks - YouTube

1. Deep Learning

• Neural Network

\[\underset{output}{y} = \overset{neural~~ network~~~~~~~~~~~~}{h(\underset{input}{x})}\]

• Deep Learning

\[h = h_L \circ h_{L-1} \circ \cdots \circ h_1\]

• Deep learning can solve any problem we want , if we have enough data, by universal approximation theorem.

2. Symmetry

• Symmetry of data is needed. For example, for 3d image data analysis, even if one object if rotated or shifted, model should suggest same result(invariant to shift & rotation & translation ..)

• Encoding symmetry as invariance under a group

\[y = h(g \cdot x) = h(x) ~~for~~all ~~g \in \mathcal{G}, x\in \mathcal {X}\]

• Preserving Symmetry with equivariance

\[y = h(g \cdot x) ~~for~~all ~~g \in \mathcal{G}, x\in \mathcal {X}\]

$\rightarrow$ transforming input is identical to transforming output, which is somehow symmetric

• Fact : Equivariance is transitive

\[h_l ~~is~~equivariant ~~\rightarrow ~~h_L \circ \cdots \circ h_1 ~~is~~equivariant\]

• Therefore, if each neural network is equivariant, the deep learning method is equivariant

  
  

3. Why symmetry?

• Encoding symmetry in network architecture is a good thing
  • Reduction in dimension of parameter space through weight sharing
  • capturing structure at multiple scales via pooling

4. Permutation Invariant data

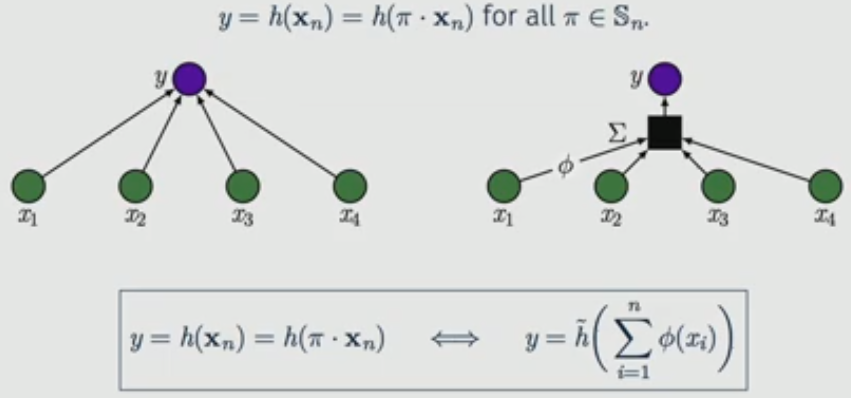
• There is a magical function $\tilde{h}$ and $\phi$ that satisfy the above equivalency.

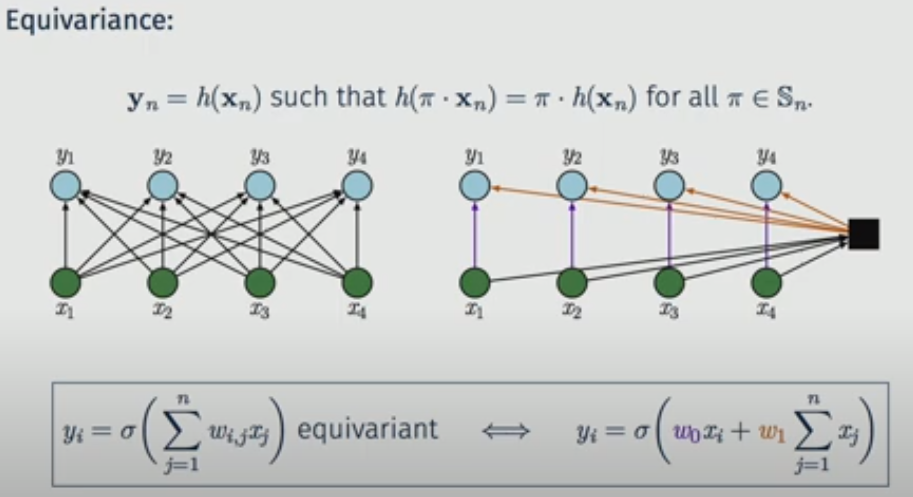
• The above shows that there is a weight sharing in case of equivariance

5. Statistical models and symmetry

• How we understand the symmetry in statistical way?

• Consider a random sequence $\mathbf{X_n} = (X_1 , \cdots X_n), ~~X{_i \in \mathcal{X}}$.

  A statistical model of $\mathbf{X_n}$ is a family of probability distribution on $\mathcal{X}^n$

\[\mathcal{P} = \{ P_\theta : \theta \in \Omega \}\]

​ If X is assumed to satisfy a symmetry property, how is $\mathcal{P}$ restricted?

6. Exchangeable sequences \(P(X_1 ,\cdots , X_n) = P(X_{\pi (1)} , \cdots , X_{\pi (n)}) ~~for~~all ~~\pi \in \mathbb{S}_n\) Also, $\mathbf{X_{\mathbb{N}}}$ is infinitely exchangeable if this is true for all prefixes $\mathbf{X_n} \subset \mathbf{X_{\mathbb{N}}} , ~~n \in \mathbb{N}$.

• de Finetti’s Theorem :

\[\mathbf{X_{\mathbb{N}}} ~~is~~exchangeable ~~\longleftrightarrow ~~X_i \vert ~Q \overset{iid}{\sim} Q ~~for~~some~~random~~Q\]

$\longrightarrow$ If $X_i$ is conditionally $iid$ , $\mathbf{X_{\mathbb{N}}}$ is exchangeable

• Implication for Bayesian Inference:
  • our models for $\mathbf{X_{\mathbb{N}}}$ need only consist of $iid$ distributions $Q$ on $\mathcal{X}$
• Implication for bayesian stats/ML
  • Rule of thumb : randomness usually makes a problem easier : softens hard constraints
  • A lot of well-established tools for working with invariant distributions
  • Distributional symmetry decomposes the problem into

structure we care about + random noise

7. Noise oursourcing

If $X$ and $Y$ are random variables in “nice” (e.g. Borel) spaces $\chi$ and $\mathcal{Y}$, then there are a random variable $\eta \sim Unif [0,1]$ and a measurable function $h : [0,1] \times \mathcal{X} ~\rightarrow ~ \mathcal{Y}$ such that $\eta \perp X$ and \((X,Y) = (X, h(\eta, X))~~~ a.s.\)

• we can turn input into output by injecting some random noise.
• Exactly, it does not need to be normal.

8. $\mathbb{S}_n$ - invariant representation

Suppose $\mathbf{X}_n$ is an exchangeable sequence.

Then ($\pi \cdot \mathbf{X}_n , Y$ ) $\overset{d}{=}$ ($\mathbf{X_n} , Y$) for all $\pi \in \mathbb{S}_n$ if and only if there is a measurable function $\tilde{h} : [0,1] \times \mathcal{X} \rightarrow \mathcal {Y}$ such that \((\mathbf{X_n}, Y )\overset{a.s.}{=} (\mathbf{X_n} , \tilde{h} (\eta , \mathbb{M}_{\mathbf{X}_n})) ~~and~~\eta \sim Unif[0,1], ~\eta \perp \mathbf{X}_n\)

.. Some more equivalency related representation