[Ensemble] Intro to Boosting & AdaBoost

Date : 2022.04.26 Updated : 2022.04.26

참고자료

Pattern recognition and machine learning

A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting, Freund, Y., & Schapire, R. E., 1997.

AdaBoost from Scratch. Build your Python implementation of AdaBoost

1. Boosting

여러개의 base learner를 앙상블하여 결과를 도출하는데, 더 예측이 어려운 관찰치, 혹은 영역을 반복적으로 학습하는 방법.
이때 base learner가 weak learner, 즉 성능이 떨어진다 하더라도 예측이 어려운 부분에 대한 반복학습과 앙상블을 통해 높은 성능을 기대할 수 있음.
배깅과 같은 commitee 형식과의 차이점은, 전 단계 훈련을 바탕으로 데이터마다 weight를 주어서 어려운 부분을 먼저 학습한다는 것임. 이에 더해, voting 역시 weighted voting을 도입하는게 일반적.


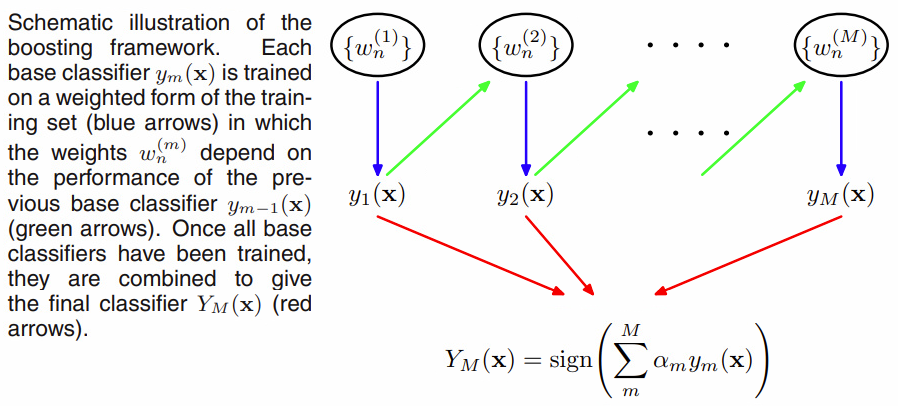출처 : Pattern recognition and machine learning

Bagging	Boosting
Overfitting 문제 발생 x	Overfitting 할 수 있음
Variance 감소	Bias & Variance 감소
Independent Base Learners	Sequential Base learners
해석이 힘듬	해석이 힘듬

2. AdaBoost (Adaptive Boosting)

데이터 정의 : ${ (X_i, y_i )}_{i=1} ^n$ , $y_i$ = {-1,1}

Step 1)

각 데이터포인트에 대해 초기에 균등하게 가중치를 분배한다 $w(x_i, y_i) = \frac{1}{n} ,~~\forall i$ Step 2)

총 m개의 약한 분류기(weak learners)에 대해 다음의 과정을 수행한다.

(1) m번째 분류기로 훈련을 한 후 오류율을 계산한다. $\epsilon_m = \frac{\sum _{i=1}^n w_i I(y_i \neq f_m(x_i))}{\sum_{i=1}^n w_i}$

(2) m번째 약한 분류기의 개별 가중치 $\theta_m$을 다음의 식에 따라 계산한다. $\theta_m = ln (\frac{1- \epsilon_m}{\epsilon_m})$ 이때, (2)의 개별 가중치 계산식에 따라 분류 정확도가 50% 이상인 경우 가중치는 양수가 되고 각 개별 분류기가 정확할수록 가중치가 커진다.

반대로 정확도가 50% 미만인 분류기의 경우 가중치는 음수가 되는데 이는 정확도가 50% 미만인 경우 음의 가중치로서 최종 예측에 반영이 됨을 의미한다.

즉, 50% 정확도를 가진 분류기는 아무런 정보를 추가하지 않으므로 최종 예측에 영향을 주지 않는 반면, 정확도가 40%인 분류기는 음의 가중치로 페널티를 가지면서 최종 예측에 기여하게 된다.

(3) 각 데이터별 가중치를 업데이트한다. ${\large w_{m+1} (x_i, y_i) = \frac{w_m (x_i, y_i) exp(- \theta_m y_i f_m(x_i))}{Z_m}}$ 이때 $Z_m$은 가중치 총합이 1이 되도록 하는 Normalizing factor다.

만일 예측이 잘못된다면 $\theta_m$이 작아지고, 가중치는 그만큼 커지게 된다. 즉, 약한 데이터에 가중치를 좀 더 줘서 학습을 하게 된다.

Step 3)

각 분류기의 가중합을 통해 최종 예측치를 얻는다. $F(x) = sign (\sum _{m=1}^M \theta_m f_m(x))$

3. AdaBoost code from scratch

Code from AdaBoost from Scratch. Build your Python implementation of AdaBoost

1. Some functions before AdaBoost

# Compute error rate, alpha and w
def compute_error(y, y_pred, w_i):
    '''
    Calculate the error rate of a weak classifier m. Arguments:
    y: actual target value
    y_pred: predicted value by weak classifier
    w_i: individual weights for each observation
    
    Note that all arrays should be the same length
    '''
    return (sum(w_i * (np.not_equal(y, y_pred)).astype(int)))/sum(w_i)

def compute_alpha(error):
    '''
    Calculate the weight of a weak classifier m in the majority vote of the final classifier. This is called
    alpha in chapter 10.1 of The Elements of Statistical Learning. Arguments:
    error: error rate from weak classifier m
    '''
    return np.log((1 - error) / error)

def update_weights(w_i, alpha, y, y_pred):
    ''' 
    Update individual weights w_i after a boosting iteration. Arguments:
    w_i: individual weights for each observation
    y: actual target value
    y_pred: predicted value by weak classifier  
    alpha: weight of weak classifier used to estimate y_pred
    '''  
    return w_i * np.exp(alpha * (np.not_equal(y, y_pred)).astype(int))

2. Class Define

# Define AdaBoost class
class AdaBoost:
    
    def __init__(self):
        self.alphas = []
        self.G_M = []
        self.M = None
        self.training_errors = []
        self.prediction_errors = []

    def fit(self, X, y, M = 100):
        '''
        Fit model. Arguments:
        X: independent variables - array-like matrix
        y: target variable - array-like vector
        M: number of boosting rounds. Default is 100 - integer
        '''
        
        # Clear before calling
        self.alphas = [] 
        self.training_errors = []
        self.M = M

        # Iterate over M weak classifiers
        for m in range(0, M):
            
            # Set weights for current boosting iteration
            if m == 0:
                w_i = np.ones(len(y)) * 1 / len(y)  # At m = 0, weights are all the same and equal to 1 / N
            else:
                # (d) Update w_i
                w_i = update_weights(w_i, alpha_m, y, y_pred)
            
            # (a) Fit weak classifier and predict labels
            G_m = DecisionTreeClassifier(max_depth = 1)     # Stump: Two terminal-node classification tree
            G_m.fit(X, y, sample_weight = w_i)
            y_pred = G_m.predict(X)
            
            self.G_M.append(G_m) # Save to list of weak classifiers

            # (b) Compute error
            error_m = compute_error(y, y_pred, w_i)
            self.training_errors.append(error_m)

            # (c) Compute alpha
            alpha_m = compute_alpha(error_m)
            self.alphas.append(alpha_m)

        assert len(self.G_M) == len(self.alphas)
        

    def predict(self, X):
        '''
        Predict using fitted model. Arguments:
        X: independent variables - array-like
        '''

        # Initialise dataframe with weak predictions for each observation
        weak_preds = pd.DataFrame(index = range(len(X)), columns = range(self.M)) 

        # Predict class label for each weak classifier, weighted by alpha_m
        for m in range(self.M):
            y_pred_m = self.G_M[m].predict(X) * self.alphas[m]
            weak_preds.iloc[:,m] = y_pred_m

        # Calculate final predictions
        y_pred = (1 * np.sign(weak_preds.T.sum())).astype(int)

        return y_pred

3. Implementation

from sklearn.datasets import load_digits
from sklearn import metrics
import pandas as pd


digits = load_digits()
train_size = 1500
train_x, train_y = digits.data[:train_size], digits.target[:train_size]
test_x, test_y = digits.data[train_size:], digits.target[train_size:]

ada = AdaBoost()
ada.fit(train_x , train_y)

# Predict on test set
y_pred = ada.predict(test_x)

4. AdaBoost code from sklearn

1. Load data & packages

# Libraryies and data loading

from sklearn.datasets import load_digits
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn import metrics
import matplotlib.pyplot as plt
import numpy as np

digits = load_digits()
train_size = 1500
train_x, train_y = digits.data[:train_size], digits.target[:train_size]
test_x, test_y = digits.data[train_size:], digits.target[train_size:]
np.random.seed(123456)

2. Ensemble

# Create the ensemble
ensemble_size = 200
ensemble = AdaBoostClassifier(DecisionTreeClassifier(max_depth = 3),
                              algorithm = 'SAMME',
                              n_estimators = ensemble_size)
ensemble.fit(train_x, train_y)

3. Evaluation

# Evaluation
ada_digit_predictions = ensemble.predict(test_x)
ada_digit_acc = metrics.accuracy_score(test_y, ada_digit_predictions)
print("AdaBoost")
print("Accuracy: %.2f" % ada_digit_acc)
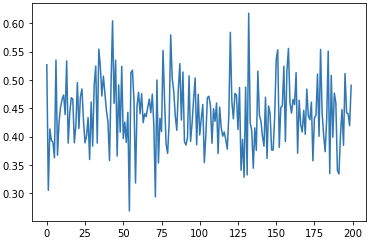
plt.plot(ensemble.estimator_errors_);

AdaBoost
Accuracy: 0.91

Share on

Twitter Facebook LinkedIn

Insik Cho