[Paper Review] Reconciling modern machine-learning practice and the classical bias–variance trade-off

1. Intro

• The classical theory : Bias- Variance trade-off

• recent practice : Double Descent

• 기존 머신러닝을 지배하는 개념은 bias-variance trade off

• 그러나 최근 딥러닝 모델에서는 매우 복잡한 모델이 test data를 잘 설명함.

  (데이터 개수보다 parameter 개수가 더 많은 경우에도 오히려 test mse가 계속 떨어짐.)

• 이를 보여주는 가상의 그래프가 위의 우측 그래프, interpolation threshold (model이 training data를 100% 설명하는 지점)을 지나가면 오히려 test error가 줄어드는 모습을 보임.

• 기존의 bias-variance trade off는 interpolation threshold 이전에서만 성립하고, 이 이후로는 오히려 parameter를 늘리는게 inductive bias를 유도하기 때문 .

---

Inductive bias

• The inductive bias (also known as learning bias) of a learning algorithm is the set of assumptions that the learner uses to predict outputs of given inputs that it has not encountered

• inductive bias란 학습 시에는 만나보지 않았던 상황에 대하여 정확한 예측을 하기 위해 사용하는 추가적인 가정을 의미.

• 흔히 말하는 Spurious한 학슴 , 과적합 등을 방지하기 위해 추가적인 가정을 하는 것을 의미합니다.
• 대표적인 예시가 CNN의 convolutional filter입니다. Fully connected layer가 데이터 전체에 대한 특성을 반영하긴 하지만, 실제로 이미지를 학습할 때는 locality를 반영하는 CNN에서의 convolutional filter가 더 특징을 잘 잡아내죠.
• 다른 예시로는 ridge나 lasso에서 주는 restriction도 일종의 inductive bias입니다.
• Regularization이라고 생각해도 무방할 듯 합니다.

---

2. Random Fourier Features

2.1. RFF?

• 논문에서는 위의 사실에 대한 실증분석으로 Random Fourie Features를 기본적으로 이용.

• RFF는 Rahimi and Recht의 2007년 논문인 “Random Features for Large-Scale Kernel Machines”에서 제시된 모델.

• RFF는 first layer의 parameter가 고정된 2-layer neural network로, 총 N개의 parameter를 가지며 다음의 형태를 띔.

\[h(x) = \sum_{k=1}^N a_k \phi(x ;v_k), ~~~where ~~~\phi (x ;v) = e^{ \sqrt{-1} <v_k,x> }\]

• 이때, $v_1 , … ,v_N$ 은 표준정규분포로부터 추출됨.

• N을 늘려가면서 모델의 complexity를 조절할 수 있기 때문에 위 모델을 예시로 사용했다고 함.

  
  

2.2. 훈련방식

• $n$개의 데이터가 주어질 때, ERM with squared loss (training MSE) 를 극소화하는 predictor $h_{n,N} \in \mathcal{H}_N$를 찾음.
• 이런 predictior 가 여러개라면 그 중 $l2 ~~ norm$이 가장 작은 predictor를 이용.

2.3. 결과

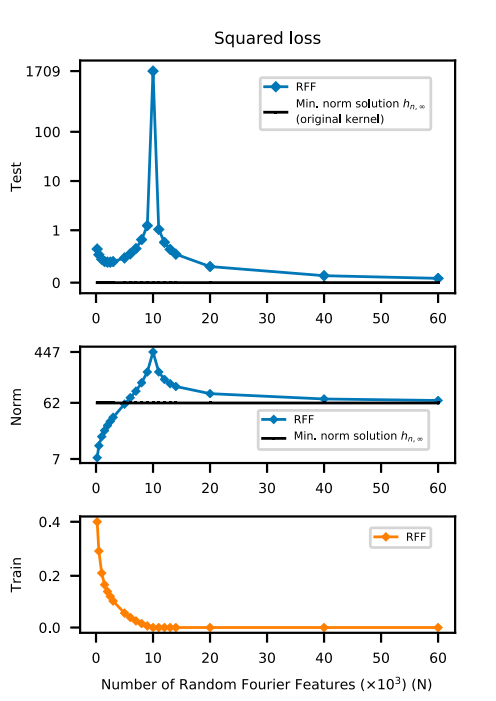
1. Test loss
   • interpolating threshold(= number of data)지점까지는 전통적인 U-shaped curve를 보이다가, 이를 지난 시점부터 하락하기 시작함.
   • 즉, interpolating threshold 지점은 완전히 과적합된 상태로, 사실상 test data에 대한 예측능력은 없는 상태임.
   • parameter가 $ \infty $ 일 때 그 test error는 최저가 됨.

1. norm

   parameter들에 대한 $l2 ~~norm$을 계산함.

   • interpolating threshold 지점까지는 norm이 계속해서 늘어남을 보여줌.
   • 그러나, 이를 지나면서 오히려 norm이 감소하고, 변수가 무한하다면 reproducing kernel Hilbert space의 minimum norm solution(위 그래프에서는 62 정도)까지 다시 감소함.

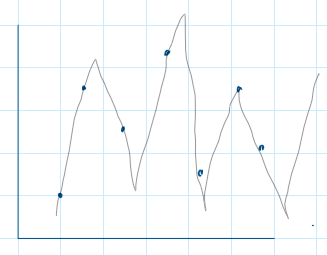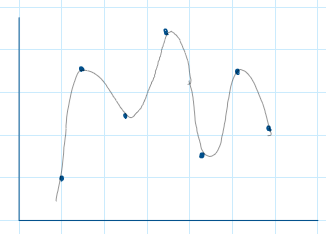paramter 숫자가 충분히 많지 않을 때	parameter 숫자가 데이터 이상으로 많아질 때

​ 위 그림은 그냥 극단적인 예시를 든 경우로, 우측과 같이 parameter가 무수히 많을 때 오히려 기존의 데이터를 설명하는 smooth한 function이 나타나고, parameter들의 l2 norm이나 test data에 대한 error가 더 감소할 수 있다는 것.

3. Fully connected neural network with SGD

• 일반적인 NN의 경우 Layer가 여러개일 때 complexity가 직관적이지 않으므로 마지막 레이어를 제외한 나머지 레이어의 parameter는 고정시켜 놓은 심플한 모델을 사용
• 결과는 비슷

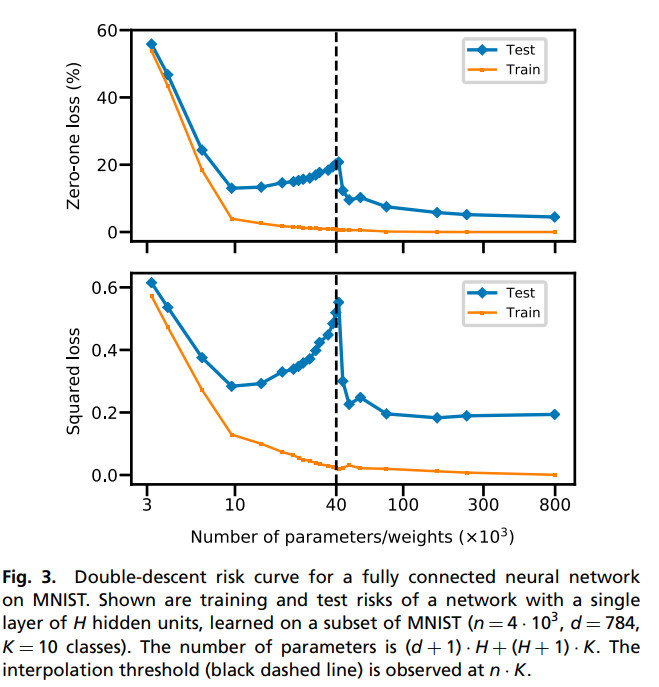
4. Tree model

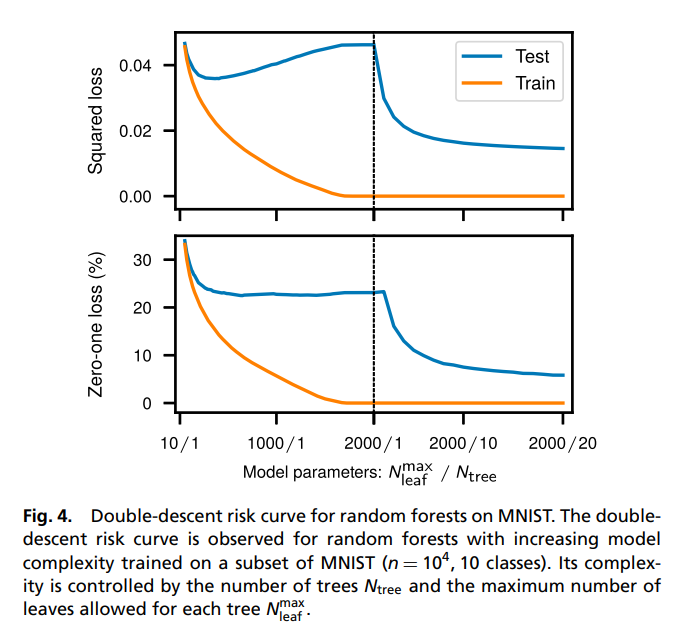
• Random forest에서도 마찬가지 결과가 나타남.
• Trees forests chickens and eggs when and why to prune trees in a random forest, 2022 논문을 참고하면 좋을 듯.

5. Conclusion

5.1. Historical Absence

• Double descent 현상은 딥러닝 이전에는 잘 연구되지 않았는데, model의 complexity를 자유자재로 조절할 수 있으면서 데이터 크기 이상으로 높은 complexity를 요구하는 모델이 거의 없었기 때문임.

• 기존 통계학에서 높은 complexity를 요구하는 모델은 보통 비모수 부문인데, 해당 부분에서는 regularization을 항상 사용하기 때문에 double descent가 논의된 적이 없음.

  
  

5.2. Practical considerations

• optimization 측면에서 유리할 수 있음.

• 기존 neural network에서는 global optimum이 아니라 local optimum에 수렴할 수 있기 때문에 initialisation이 중요하다.

• 그런데, over-parametrized (parameter » data)된 모델의 경우 SGD가 global optimum에 수렴할 수 있음.

  (관련된 논문 몇개 찾아보니, 항상 그런건 아니고 그런 경우가 있고, 여기도 연구 진행중인 것 같음. )