[GAN] Gumbel Softmax

내용 참고

1. https://towardsdatascience.com/what-is-gumbel-softmax-7f6d9cdcb90e
2. Jang, Eric, Shixiang Gu, and Ben Poole. “Categorical reparameterization with gumbel-softmax.” arXiv preprint arXiv:1611.01144 (2016).
3. Maddison, Chris J., Andriy Mnih, and Yee Whye Teh. “The concrete distribution: A continuous relaxation of discrete random variables.” arXiv preprint arXiv:1611.00712 (2016).

1. Categorical variable backpropagation

$Categorical$ $(\pi_1 , \cdots , \pi_x)$ 를 훈련 목표로 하는 neural network가 있다고 하자. 이때 변수는 one-hot encoding 처리되어있다.

$Z$를 샘플링하는 가장 간단한 알고리즘은 다음과 같은데,

\(Z = onehot~~ (max\{ i \vert \pi_1 + \cdots + \pi_{i-1} \leq U \})\)

이때, $i = 1, … , x $는 클래스의 인덱스이고, $U ~ \sim ~ uniform (0,1)$인 유니폼분포이다.

위 샘플링 방식은 미분불가능하기 때문에 역전파가 되지 않은데, 이를 해결하기 위한 방법이 gumbel softmax임.

2. The Gumbel-Max trick

Gumbel max trick의 샘플링은 다음과 같다.

\(Z = onehot ~~(argmax_i~\{ G_i + log(\pi_i ) \} )\)

이때, $G_i \sim Gumbel(0,1)$로 $G$가 Standard Gumbel 분포를 따르는 i.i.d 샘플이다.

(* $ G = -log(-log(U))$ )

논문에서는 이를 $Z$의 샘플링을 refactoring 한다고 표현하는데, 이는 샘플링 과정을 independent 한 noise의 분포로 재표현하는 것을 의미한다.

3. Using sofrmax as a differentiable approximation

그러나 위에는 여전히 argmax가 들어가므로 미분불가능하다. 단지, argmax 안의 값을 고정된 분포의 함수로 나타내어 해당 부분의 미분이 쉬워졌을 뿐인다.

따라서 argmax에 대한 differentiable한 함수로 근사를 해야하는데, softmax를 사용한다.

\(y_i = exp((G_i + log \pi_i )/ \tau ) ~/~ \Sigma_j exp((G_j + log\pi_j )/ \tau)\)

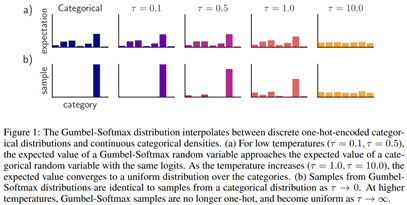
이때 $\tau$ 는 위의 샘플링이 얼마나 one-hot vector에 근접하는지를 나타내는 parameter이다.

$\tau$ -> 0 이라면 one-hot vector와 동일해지고, $\tau \rightarrow \infty$ 라면 uniform에 가까워진다.