In progress

[Paper Review] Modeling Tabular Data using Conditional GAN

Date :     Updated :

1. Challenges with GANS in Tabular Data Generation Task


1. Mixed Data types

  • Tabular data에는 discrete & continuous column이 모두 존재하기 때문에 단순하게 softmax만 사용한다거나 할 수 없음.


2. Non-Gaussian & Multimodal distributions

  • 이미지는 보통 픽셀이 가우시안과 유사한 분포를 따르기 때문에 [-1, 1]로 min-max transformation 하여 사용할 수 있음. 그렇지만 tabular data는 non-gaussian인 경우가 많기 때문에 단순한 min-max transformation을 적용할 수 없음.
  • 여기에 더해 distribution이 multimodal인 경우가 흔한데, 이 경우에는 특정 mode에 빠져버릴 수가 있음.


3. Learning from sparse one-hot-encoded vectors

  • 명목형 변수를 처리하려면 one-hot-encoding이 불가피한데, 이때 일반적으로 사용하는 softmax를 사용하면 학습이 잘 안이루어짐.
  • 예를 들어, 실제 값이 [1,0,0]인데, generator가 [0.5, 0.25, 0.25]와 같이 확률값으로 뱉어낸다면, discriminator는 그저 값이 정확하게 정수인 데이터를 골라내면 true data를 찾아낼 수 있게 됨


4. Highly Imbalanced Categorical columns

  • 많은 데이터가 highly imbalacned categorical columns를 가짐. 이로 인해 mode collapse로 이어질 수 있음.



2. Conditional Tabular GAN


  • 저자는 여러가지 방법론을 적용하여 위의 문제점들을 최대한 줄이고자 함.

Notation

  • $G$ : data synthesizer

  • $T$ : Tabular data

  • $T_{syn}$ : Synthesized tabular data

  • ${ C_1 , \cdots , C_{N_c } }$ : $N_c$ continuous columns of $T$

  • ${ D_1 , \cdots , D_{N_d } }$ : $N_d$ disicrete columns of $T$

  • $x_1 \oplus x_2 \oplus \cdots $ : concatenate vectors $x_1 , x_2 $

  • gumbel$_\tau (x)$ : apply Gumbel softmax with parameter $\tau$ on a vector $x$

  • leaky$_\gamma (x)$ : apply a leaky ReLU activation on $x$ with leaky ratio $\gamma$

  • FC$_{u \rightarrow v} (x)$ : apply a linear transformation on a $u$-dim input to get a $v$-dim output


1. Mode - Specific Normalization

  • 앞서 언급한 challenge 중 2. Multimodal distribution 문제를 해결하기 위한 방안.

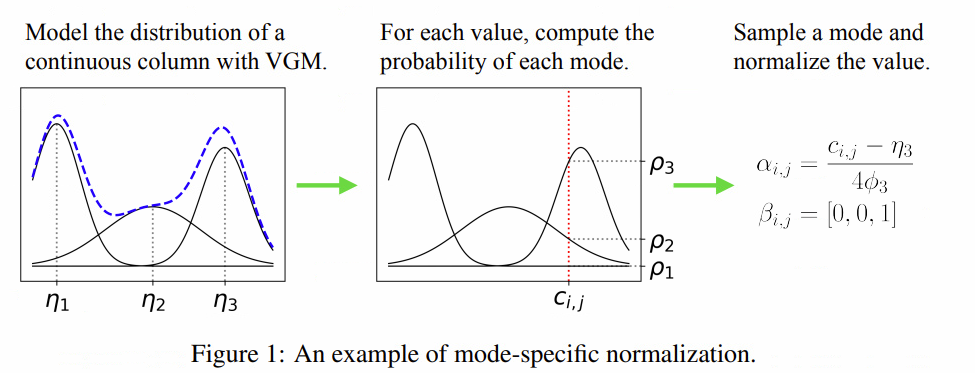
image-20221126012132873

  • 다음의 3가지 스텝을 통해서 이루어짐.

    step 1) 연속형 변수 $C_i $에 대하여 VGM(Variational Gaussian Mixtue model)을 적합하여 gaussian mixture 분포를 추정하고 mode의 수 $m_i $를 추정한다.


    예를 들어 위의 첫번째 그림에서 파란 점선이 실제 그래프인데, 이는 3가지 봉우리를 가진다. VGM을 통해 3개의 mode를 가지는 mixed normal로 추정을 해낸다. 각 정규분포의 가중치, 평균과 표준편차를 $(\mu_i ,\eta _i , \phi_i )$ 라고 할 때, 추정된 분포는 다음과 같이 나타낸다. \(\mathbb{P}_{C_i} = \sum _{k=1} ^3 \mu_k \mathcal{N} (c_{i,j} ; \eta_k , \phi _k)\)


    step 2) $C_i$ 의 개별 값 $c_{i,j}$에 대하여 해당 값이 각 mode에 할당 될 확률을 계산한다.

    이는 위의 두번째 그림과 같으며, 확률은 다음과 같이 계산한다. \(\rho_k = \mu_k \mathcal{N} (c_{i,j} ; \eta_k , \phi_k )\)


    step 3) 추정된 평균, 표준편차, mode를 이용하여 정규화를 진행한다.

    이때 continuous column의 데이터는 $\alpha_{i,j} \oplus \beta_{i,j}$로 나타내는데, $\alpha_{i,j}$ 와 $\beta_{i,j}$는 다음과 같다. $\beta_{i,j}$ : step 2)에서 계산한 할당 될 확률에 기반하여 mode 선택. 위의 그래프에서는 $\rho_3 $가 가장 컸으므로 [0,0,1]

    $\alpha_{i,j}$ : 선택된 mode의 값을 바탕으로 정규화 시행. $\alpha_{i,j} = \frac{c_{i,j} - \eta_3}{4 \phi_3}$


  • 위 과정을 통해 얻은 값들을 concatenate하여 데이터로 사용. \(\mathbf{r} _j = \alpha_{1,j} \oplus \beta_{1,j} \oplus \cdots \oplus \alpha_{N_c,j} \oplus \beta_{N_c ,j} \oplus \mathbf{d}_{1,j }\oplus \cdots \oplus \mathbf{d}_{N_d ,j }\)



2. Conditional Generator and Training by Sampling

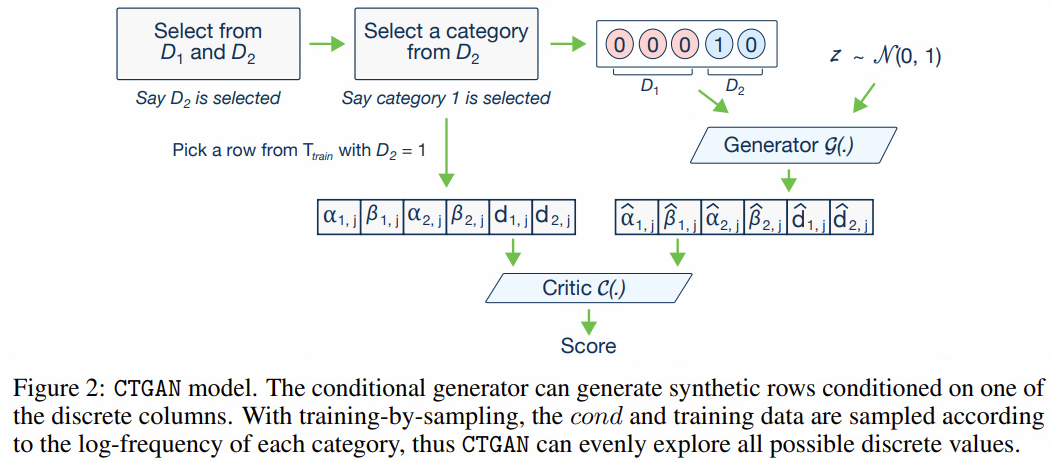
image-20221126012416135


  • 데이터를 완전히 랜덤으로 투입하게 되면, 위에서 언급한 4번째 문제인 4. Highly imbalanced categorical columns로 인해 minority class에 대한 훈련이 잘 안 이루어지게 된다.
  • 따라서, minority class에 대한 sampling이 조금 더 많이 이루어져야지 고른 훈련이 진행될 수 있다.
  • 단, 만일 uniformly 하게 훈련을 하게 된다면 기존 데이터가 가지는 특징을 반영할 수 없으므로, conditional vector와 generator loss를 바꾸고, training - by - samplin 기법을 도입하였다.


Conditional Vector

  • conditional vector를 도입하여서 데이터가 어떤 discrete value를 condition 으로 가지는지 표시한다.

    ( $ D_{i^{\star}} = k^{\star} $ )

  • $i$ 번째 discrete vector에 대해서 $k$번째 값이 1이라면, 이를 $m_i = [ 0 \cdots 0\underset{k_{th} }{1} 0\cdots 0 ]$로 표시한다.


  • 예를 들어, 2개의 discrete columns이 있고 $D_1 = { 1,2,3} ~~and ~~ D_2 = { 1,2 } $일 때, condition $D_2 = 1$은 $m_1 = [0,0,0]$ , $m_2 = [1,0]$이므로 $cond ~=~[0,0,0,1,0]$ 으로 표시한다.


Generator loss

  • 위의 conditional vector에 맞춰서 훈련이 될 수 있도록, 관련 term을 generator loss에 포함시킨다.
  • 이는 $m_{i^{\star}}$와 $\hat{d_{i^{\star}}}$ 의 cross-entropy로 나타난다.


Training by sampling

  • GAN model은 generator에 의한 조건부 분포인 $\mathbb{P}_{\mathcal{G}} (row \vert cond)$와 실제 조건부 분포인 $\mathbb{P} (row \vert cond)$ 사이의 distance를 최소화하는 방향으로 훈련한다. 이때, 올바른 훈련이 진행될 수 있도록 discrete column에서 최대한 공평하게 value들이 추출될 수 있도록 training - by - sampling을 제시한다. 해당 방법은 다음의 6가지 step에 의해서 이뤄진다.



Step 1)

$N_d $개의 0으로 구성된 mask vector $m_i$를 만든다.


Step 2)

$N_d$개의 discrete column중 하나의 column을 임의로 뽑는다(with equal probability). 위의 그림을 예시로 들자면, $N_d =2 $개의 column 중 $D_2$를 선택한다.


Step 3)

선택된 $D_{i^\star}$ column에서 가능한 값들에 대해서 PMF를 만든다. 이때 각 값의 확률은 출현빈도의 로그로 정의한다.

만일 기존의 출현 빈도를 그대로 반영하면 minority 문제가 해결이 안되고, uniquely 뽑으면 데이터의 특징을 반영할 수 없으므로 저자는 로그값을 사용함.


Step 4)

위에서 정의한 PMF에 따라서 값 하나를 추출한다. 위의 그림을 예로 들자면, $k^{\star} = 1$가 추출되었다.


Step 5)

$i^\star th$ 열에서 $k^\star th$ value를 1로 놓는다.


Step 6)

$cond = m_1 \oplus m_2 \oplus \cdots \oplus m_{N_d}$를 만든다.

위의 예시에서는 $m_1 = [0,0,0]$ , $m_2 = [1,0]$이므로 $cond ~=~[0,0,0,1,0]$ 가 된다.


3. Gumbel softmax


  • 위에 제시된 문제점 중 3. Learning from sparse one-hot-encoded vectors를 해결하기 위해 Gumbel Softmax를 사용하였다.

  • Gumbel softmax의 형태는 다음과 같다. \({ \large y_i = \frac{exp(\frac{G_i + log \pi_i }{ \tau } ) } {\sum_j exp(\frac{G_j + log\pi_j } {\tau})} }\) (참고 : [GAN] Gumbel Softmax - Data Science (whatsdata.github.io))

  • $\tau$ 는 gumbel softmax가 얼마나 one-hot encoding에 가까워지는지 나타내며, $\tau \rightarrow 0$ 라면 one-hot vector에 가까워진다. 또한, 기본적으로 softmax의 형태이므로 differentiable하기 때문에 학습이 가능하다.

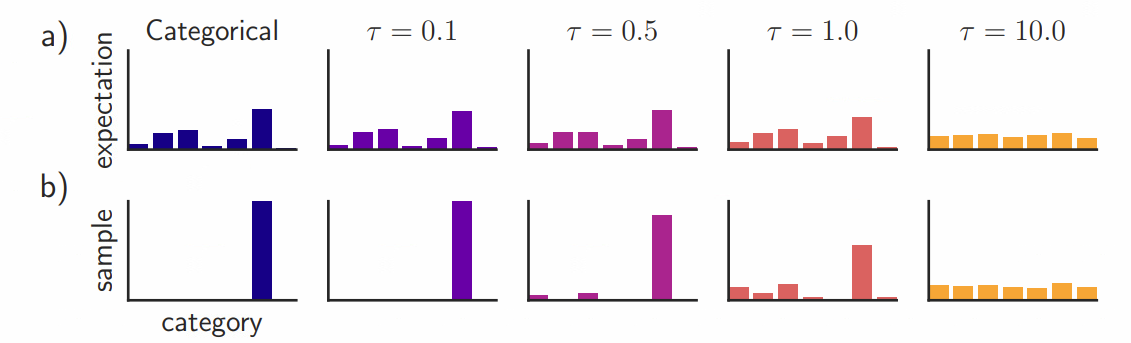
    image-20221126013058200


4. Network Structure

4.1. Generator

  • tanh, gumbel 등 여러가지 activation function을 사용하여 1. Mixed Data types 문제를 해결하였다.

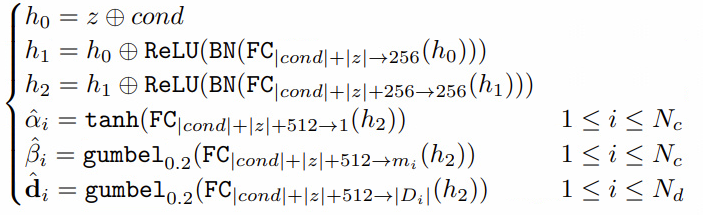
    image-20221126013319947

  • $\alpha_i$ 는 continuous 값을 가지므로 $tanh$을 사용하며,
  • $\beta_i $와 $\mathbf{d}_i$ 는 one hot 형태를 가지므로 gumbel softmax를 사용한다.


4.2. Discriminator

  • discriminator에서는 mode collapse를 막기 위해 pacgan 형태의 discriminator를 사용한다.

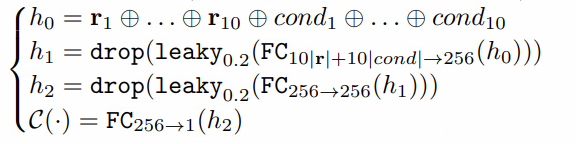
    image-20221126013606760

  • pacgan이란 여러개의 데이터를 하나의 pac으로 구성해서 discriminator에 한꺼번에 집어넣는 것이다.
  • 본 모델에서는 10개의 데이터를 하나의 pac으로 구성해서 discriminator에 넣는다.


4.3. Loss

  • Loss function으로는 WGAN-GP를 사용한다.



3. Evaluation metric

  • Simulated data와 real data를 이용.
  • Simulated data
    • Gaussian mixture model
    • Bayesian network
  • real data
    • UCI ML repository data


3.1. Likelihood fitness metric

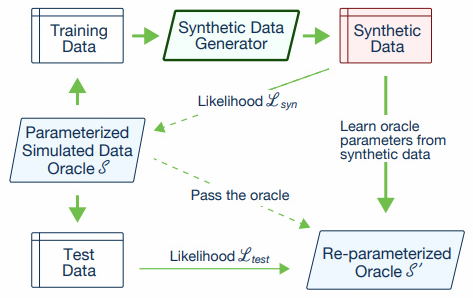
image-20221126014057244

  • Simulated data를 사용
  • data를 train data와 test data로 나눈 후, train data를 이용하여 cTGAN을 학습한다.
  • 학습된 모델을 통해 Synthetic data를 생성한후, 생성된 데이터와 기존의 train data 사이의 Likelihood를 계산한다. ($L_{sync}$)
  • 해당 Likeliihod는 overgitting 될 수록 좋아지므로, 대신 test data와의 likelihood도 계산한다. ($L_{test}$ )


3.2. Machine learning efficacy

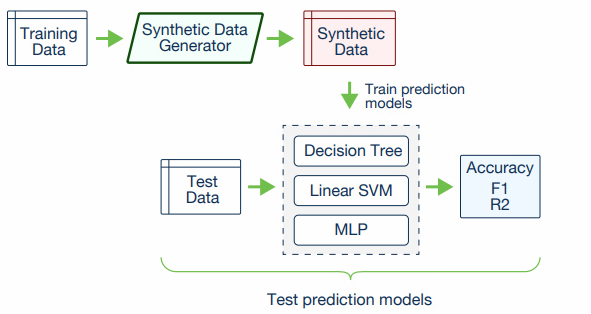
image-20221126014108043

  • Real data를 사용한다.
  • Synthetic data를 통해 학습한 machine learning score와 test data를 통해 학습한 score의 차이를 비교한다.



4. Experiment Result

4.1. Comparament to benchmarking result

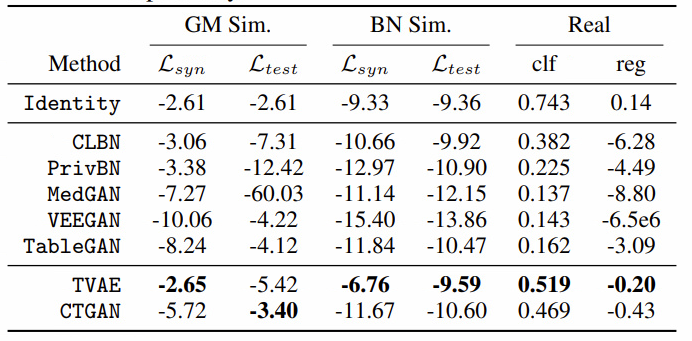
image-20221126013945306


  • Likelihood fitness metric

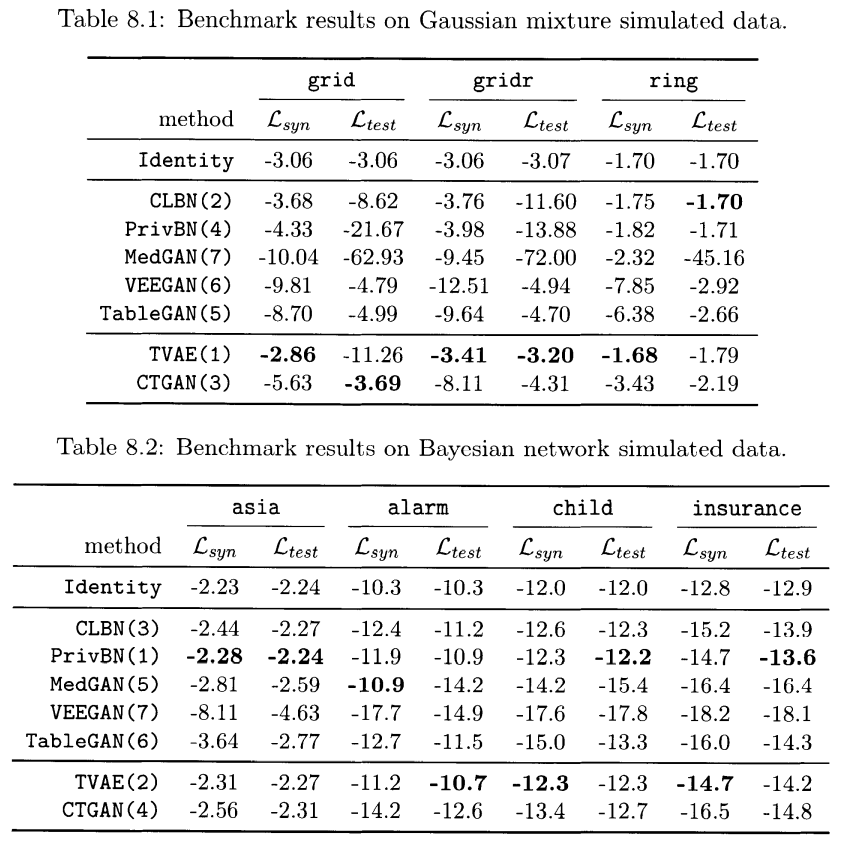
image-20221130120412588


  • Machine learning efficacy

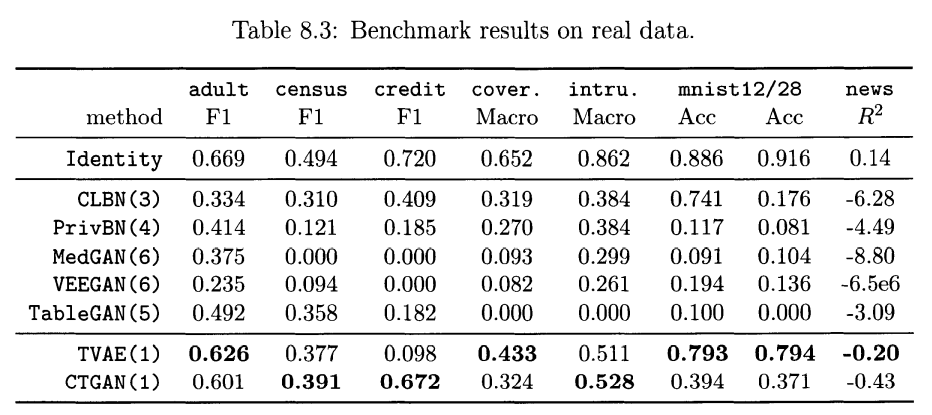
image-20221130120324293


4.2. Ablation study

image-20221126014017330

Tags:

Categories:

Date :

Leave a comment

최근 글 10 개 :)