[High Dimensional Statistics] Uniform Laws of large numbers

References

• Yonsei univ. STA9104 : Statistical theory for high dimensional and big data
• High-Dimensional Statistics : A Non-Asymptotic Viewpoint, 2017, Martin J. Wainwright

​ Uniform laws have been investigated in part of empirical process theory and have many applications in statics. in contrast to the usual law of large numbers that applies to a fixed sequence of random variables, uniform laws of large numbers provide a guarantee that holds uniformly over collections of random variables. A goal of this post is to introduce tools for studying uniform laws with an emphasis on non-asymptotic results.

​

Summary about convergence

- Pointwise Convergence
Let $(N, d)$ be metric space. For sequence of functions
$$ \begin{align} &f_n : A \longrightarrow N, \quad n =1, \cdots , n \\ &f\,\,\, : A \longrightarrow N \end{align} $$ The sequence of functions are said to converge pointwise to the function $f$, if for each $x \in A$, $f_n (x) \longrightarrow f(x)$,
i.e. for each $x\in A$ and $\epsilon >0$, $\exists L = L(x, \epsilon)$ such that $d(f_n (x), (x)) \leq \epsilon , \quad \forall n \geq L$

- Unform Convergence
Let $(N, d)$ be metric space. For sequence of functions
$$ \begin{align} &f_n : A \longrightarrow N, \quad n =1, \cdots , n \\ &f\,\,\, : A \longrightarrow N \end{align} $$ The sequence of functions are said to converge pointwise to the function $f$, if for each $x \in A$, $f_n (x) \longrightarrow f(x)$,
i.e. for each $x\in A$ and $\epsilon >0$, $\exists L = L( \epsilon)$ such that $d(f_n (x), (x)) \leq \epsilon , \quad \forall n \geq L$
,which is same with
$$ \underset{x \in A} {sup} \quad d(f_n (x) , (x)) < \epsilon, \quad \forall n \geq L $$ - some relations
1. The derivatives of a pointwise convergent sequence of functions do not have to converge.

consider $X = \mathbb{R} $ and $f_n (x) = \frac{1}{n} sin(n^2 x)$ . Then,
$$ \underset{n \rightarrow \infty}{lim} f_n (x) = 0 $$ So, the pointwise limit function is $f(x)=0$; the sequence of functions converges to 0. What about the derivatives of the sequence?
$$ f_n '(x) = n cos (n^2 x) $$ and for most $x \in \mathbb{R}$, above derivative is unbounded, which means that it does not converge.
2. The integrals of a pointwise convergent sequence of functions do not have to converge.

Consider $X= [0,1],$ and $f_n (x) = \frac{2 n^2 x}{(1+n^2 x^2)^2}.$ Then,
$$ lim_{n \rightarrow =\infty} f_n (x) = 0 $$ However, the integrals are
$$ \int^1_0 \frac{2 n^2 x dx}{(1+n^2 x^2)^2} \overset{u = 1+ n^2 x^2}{=} \int ^{1+n^2}_{1 }\frac{du}{u^2} = 1 - \frac{1}{1+n^2} $$ Therfore, even thought $lim_{n \rightarrow =\infty} f_n (x) = 0$ for all $x \in X$, the intergral is 1 as $n \rightarrow \infty$
3. The limit of a pointwise convergent sequence of continuous functions does not have to be contuniuous

$A = [ 0, 1]$ and $f_n(x) = x^n $. Then,
$$ \underset{n \rightarrow \infty}{f_n (x)} = f(x) = \cases{0 \quad (0 \leq x <1)\\ 1 \quad (x=1)} $$
It satisfies pointwise convegence, but limit is not continuous
4. The uniform convergence implies pointwise convergence, but not the other way around.

Same example with above one.
If $f_n(x)$ converges uniformly, then the limit function must be $f(x) =0$ for $x \in [0,1)$ and $f(1) = 1$. Uniform convergence implies that for any $\epsilon >0 $ there is $N_\epsilon \in \mathbb{N}$ such that $\vert x^n - f(x)\vert$ for all $n \geq N_\epsilon$ . Then, consier $\epsilon = \frac{1}{2}$. Then, there is $N $ such that for all $n \geq N$, $\vert x^n - f(x) \vert < \frac{1}{2}$. If we choose $n=N$ and $x = (\frac{3}{4})^N$, $f(x) = 0 $ and thus
$$ \vert f_N (x) - f(x) \vert = \frac{3}{4} $$
contradicting our assumption.

1. Motivation

1.1. Almost sure convergence

​ Before start of demonstration, I will talk about two probabilistic convergence, Almost sure convergence and Convegence in probability .

1.1.1. Convergence in probability

For $X_n $ and $X$ on ($\Omega, \mathcal{F}, \mathbb{P}$), A sequence of random variables converges in probability to a random variable X, denoted by $X_n \overset{P}{\rightarrow} X $ if

\[\underset{n \rightarrow \infty } {lim}\mathbb {P} (s \in S : \vert X_n(s) - X(s) \vert <\epsilon) \rightarrow 1 , \quad \forall \, \epsilon >0\]

,where $S$ is an underlying sample space.

1.1.2. Almost sure convergence

For $X_n $ and $X$ on ($\Omega, \mathcal{F}, \mathbb{P}$), A sequence of random variables converges almost surely to a random variable X, denoted by $X_n \overset{a.s.}{\rightarrow} X $ if

\[\mathbb {P} (s \in S :\underset{n \rightarrow \infty } {lim} \vert X_n(s) - X(s) \vert <\epsilon) \rightarrow 1 \quad\longleftrightarrow \quad \sum_{n=1}^\infty I(\vert X_n (s) - X(s) \vert >\epsilon ) < \infty , \quad \forall \, \epsilon >0\]

,where $S$ is an underlying sample space.

Here, second inequality is true by Borel- Cantelli lemma.

1.1.3. Comparison of concepts

To understand the difference, Law of large number is one example.

I referred random variable - Convergence in probability vs. almost sure convergence - Cross Validated (stackexchange.com) for explanation here.

Weak law of large numbers, which states about convergence in probability of $\bar{X} = \sum_{i=1}^n X_i /n$, says that a large proportion of the sample paths will be in the bands on the right-hand side, at time $n$. It just means that the probability that particular curve to be located in curve will approaches to one.

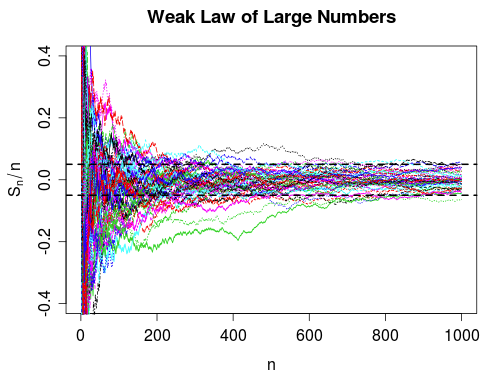
However, in case of strong law of large numbers, a curve surely will be in bands.

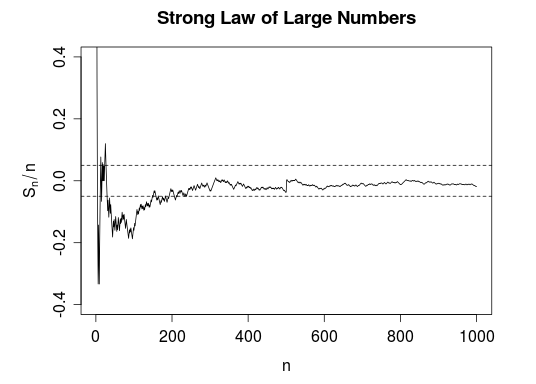
The difference also can be seen from other representations of definition.

SLLN

\[\mathbb {P} (s \in S :\underset{n \rightarrow \infty } {lim} \vert X_n(s) - X(s) \vert <\epsilon) \rightarrow 1 , \quad \forall \, \epsilon >0 \quad \longleftrightarrow \underset{n \rightarrow \infty } {lim} \mathbb {P} (s \in S :sup_{m \geq n}\vert X_n(s) - X(s) \vert >\epsilon) \rightarrow 0 , \epsilon >0\]

WLLN

\[\underset{n \rightarrow \infty } {lim}\mathbb {P} (s \in S : \vert X_n(s) - X(s) \vert >\epsilon) \rightarrow 0 , \quad \forall \, \epsilon >0\]

, $X_n = \frac{\sum_{i=1}^n X_i}{n}$ in case of law of large numbers.

1.2. Cumulative distribution functions

Let $X$ be a random variable with its cumulative distribution function, $F(t) = \mathbb{P}(X \leq t), \quad \forall t\in \mathbb{R}$. Then, natural estimate of $F$ is the empirical CDF given by,

\(\hat{F}_n (t) = \frac{1}{n} \sum_{i=1}^nI_{(-\infty, t\rbrack}(X_i)\) Here, empirical CDF is unbaised estimator for pupulation CDF because

\[\begin{align} \mathbb{E} [I_{( -\infty, t\rbrack}(X)] &= P(X \leq t) \times 1 + P(X \geq t) \times 0 \\ &= F(t)\\ \end{align}\]

Moreover, uniform convergence of CDF is proved by Glivenko-Cantelli Theorem.

Uniform convergence is important because many estimation problem start from functional of CDF. For example,

• Expectation Functionals

\[\gamma_g (F) = \int g(x) dF(x)\]

which is estimated by plug-in estimator given by $\gamma_g(\hat{F_n}) = \frac{1}{n} \sum_{i=1}^n g(X_i)$

• Quantile functionals

\[Q_\alpha (F) = \inf \{ t\in \mathbb{R} : F(t) \geq \alpha \}\]

which is estimated by plug-in estimator given by $Q_\alpha (\hat{F}_n) = \inf { t\in \mathbb{R} : \hat{F(t)} \geq \alpha }$

Above estimators are justified by continuity of a functional. That is, once we know that $\lVert\hat{F_n} -F \rVert_{\infty}$ $\rightarrow $ 0 in probability, then we also have the result that $\vert \gamma( \hat{F_n} ) - \gamma(F) \vert \rightarrow 0$ for a functional $\gamma$, whenvert $\gamma$ is a continuous with respect to the sup-norm : $\lVert F- G \rVert_{\infty} = sup_{t\in \mathbb{R}} \vert F(t)- G(t) \vert$

​ continuous with respect to the sup-norm

​ we say that the function $\gamma$ is continuous at $F$ in the sup-norm if, for all $\epsilon >0$, there exists a $\delta >0$ such that $\vert \vert F-G \vert \vert _{\infty} \leq \delta$ implies that $\vert \gamma(F) - \gamma (G) \vert \leq \epsilon$.

1.3. Uniform laws for more general function classes

​ Let $\mathcal{F}$ be a class of integrable real-valued functions with domain $\mathcal{X}$ and let ${ X_i }_{i=1}^n$ be a collection of i.i.d. samples from some distribution $\mathbb{P}$ over $\mathcal{X}$. consider the random variable

\[\vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert _{\mathcal{F}} = \underset{f \in \mathcal{F}}{sup} \bigg\vert \frac{1}{n} \sum_{i=1}^n f(X_i) - \mathbb{E} [f(X)] \bigg\vert\]

,which measures the absolute deviation between the sample average and the population average, uniformly over the claff $\mathcal{F}$. we say that $\mathcal{F}$ is a Glivenko-Cantelli class for $\mathbb{P}$ if $ \vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert _{\mathcal{F}}$ converges to zero in probability as $n \rightarrow \infty$.

• Empirical CDFs

\[\mathcal{F} = \{ I_{( -\infty , t \rbrack } : t \in \mathbb{R}\}\]

We could see $\mathcal{F}$ satisfies the definition of Glivenko-Cantelli class by Glivenko-Cantelli Theorem. Therefore, $\mathcal{F}$ is Glivenko-Cantelli class

• Failure of uniform law

Not all classes of functionals are Glivenko-Cantelli. Let $\mathcal{S}$ be the class of all subsets $S$ of $\lbrack 0,1\rbrack $ such that the subset $S$ has a finite number of elements, and consider the function class $\mathcal{F}_S = { I_S (\cdot) : S \in \mathcal{S} }$ of indicator functions of such sets. Suppose that samples are drawn from continuous distributions over $\lbrack 0,1\rbrack $ such that $\mathbb{P}(S) =0$ for any $S \in \mathcal{S}$ . on the other hand, for any positive interger $ n \in \mathbb{N}$, the discrete set $S_n = { X_1 , \cdots, X_n }$ belongs to $\mathcal{S}$, and moreover, by definition of the empirical distribution, we have

\[\frac{1}{n} \sum_{i=1}^n I_{S_n} (X_i) = 1\]

Therefore, we conclude that

\[\lVert \mathbb{P} { _\mathcal{n}} - \mathbb{P} \rVert = 1-0 = 1\quad for\,\,\, every \,\,\,positive\,\,\, integer \,\,\,n\]

, and thereby $\mathcal{F}_\mathcal{S}$ is not a Glivenko-Cantelli class for continuous distributions.

1.4. Empirical risk minimization

• Suppose that samples are drawn i.i.d. according to a distribution $\mathbb{P}_{\theta^\star}$ for som fixed but unknown $\theta^\star \in \Omega$.
• A standard approach to estimating $\theta^*$ is based on minimizing a cost function $\mathcal{L}_\theta (X)$ that measures the fit between a parameter $\theta \in \Omega$ and the sample $X \in \mathcal{X}$.
• We then obtain some estimate $\hat{\theta}$ that minimizes the empirical risk defined as

\[\hat{R}_n (\theta , \theta^\star) = \frac{1}{n} \sum_{i=1}^n \mathcal{L}_{\theta} (X_i)\]

​ One specific example is Maximum Likelihood Estimator.

• In contrast, the population risk is defined as

\[R(\theta , \theta^\star) = \mathbb{E}_{\theta^\star} [ \mathcal{L}_\theta (X)],\]

​ where expectation is taken over a samples $X \sim \mathbb{P}_{\theta^\star}$. The statistical question of interest is how to bound the $excess \,\,\, risk$:

\[E(\hat{\theta}, \theta^\star) = R(\hat{\theta}, \theta^\star) - \underset{\theta \in \Omega}{\inf} R(\theta, \theta^\star)\]

​ Which is risk from estimor of empirical risk minimization and true unknown estimator is how small compared to pupulation risk.

​ For simplicity, assume that there exists some $\theta_0 \in \Omega$ such that $R(\theta_0, \theta^\star) =\underset{\theta \in \Omega}{\inf} R(\theta, \theta^\star)$

With the notation , the exess risk can be decomposed as

\[E(\hat{\theta}, \theta^\star) = \underbrace{\{ R(\hat{\theta}, \theta^\star)-\hat{R}_n (\hat{\theta} , \theta^\star) \}}_{T_1} + \underbrace{\{ \hat{R}_n(\hat{\theta}, \theta^\star)-\hat{R}_n ((\theta_0 , \theta^\star) \}}_{T_2} + \underbrace{\{ \hat{R_n} (\theta_0 , \theta^\star) - R(\theta_0, \theta^\star)\}}_{T3}\]

By the definition of $\hat {\theta}$, $T_2<0$. For the $T_1$,

\[T_1 = \mathbb{E}_{X} [\mathcal{L} _\widehat{\theta}(X)\rbrack - \frac{1}{n} \sum_{i=1}^n {\mathcal{L} _{\widehat{\theta}} (X_i)}\]

, uniform law of large numbers over the cost function $\mathcal{F}(\Omega) = { x \rightarrow \mathcal{L}_\theta (x), \theta \in \Omega_0 }$ is required. With this notation,

\[T_1 \leq \underset{\theta \in \Omega_0}{sup} \bigg\vert \frac{1}{n}\mathcal{L}_{\theta} (X_i) - \mathbb{E}_X [\mathcal{L}_\theta (X)]\bigg\vert = \vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert_{\mathcal{F}(\Omega)}\]

Also, for the $T_3$ , is dominated by this quantity,

\[T_3= \frac{1}{n} \sum \mathcal{L}_{\theta_0} (X_i) - \mathbb{E}_x \lbrack\mathcal{L}_{\theta_0} (X)\rbrack\]

It is also dominated by above quantity,

\[E(\hat{\theta}, \theta^\star) \leq 2\vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert_{\mathcal{F}(\Omega)}\]

It states that the central challenge in analyzing estimators based on empirical risk minimization is to establish a uniform law of large numbers for the loss class $\mathcal{F}(\Omega)$.

2. A uniform law via Rademacher complexity

2.1. Definition of Rademacher complexity

• Empiricial Rademacher complexity of the function class $\mathcal{F}$

For any fixed collection $x_1^n = (x_1 ,\cdots ,x_n)$, consider the subset of $\mathbb{R}^n$ given by

\[\mathcal{F} (x_1^n) = \{ (f(x_1), f(x_2) , \cdots f(x_n )) : f \in \mathcal{F} \}\]

The empirical Rademacher complexity is given by

\[\mathcal{R}(\mathcal{F}(x_1^n)/n) = \mathbb{E} _{\epsilon} \bigg\lbrack \frac{1}{n} \sum_{i=1}^n \epsilon_i f(x_i) \bigg\rbrack\]

, where $\epsilon_1, \cdots , \epsilon_n$ are $i.i.d.$ Rademacher random variables.

• Rademacher complecity of the function class $\mathcal{F}$

​ By taking expectation on empirical rademacher complexity,

\[\mathcal{R}(\mathcal{F}) = \mathbb{E} _{X,\epsilon } \bigg\lbrack \frac{1}{n} \sum_{i=1}^n \epsilon_i f(x_i) \bigg\rbrack\]

​ By the form of formula, note that the Rademacher complexity is the maximum correlation between the vector $(f(x_1), f(x_2) , \cdots f(x_n ))$ and the noise vector ($\epsilon_1, \cdots , \epsilon_n$). Also, if a function class is extremply large, then we can always find a function that has a high correlation with a randomly drawn noise vector. Conversely, if function size is too small, correlation will be small.

​ In this sense,the Rademacher complexity measures the size of a function class and it plays a key role in establishing uniform convergence resuts.

2.2. Glivenko-Cantelli propety

• $Define)$ a function class $\mathcal{F}$ IS $b$-uniformly bounded if $\vert \vert f \vert \vert_{\infty} \leq b$ for all $f \in \mathcal{F}$.

• Theorem (Glivenko-Cantelli property) For any $b$-uniformly bounded class of function class $\mathcal{F}$ , any positive integer $n \geq 1$ and any scale $\delta \geq0$, we have

\[\vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert _{\mathcal{F}} \leq 2 \mathcal{R}_N (\mathcal{F}) + \delta\]

​ with $\mathbb{P}$ -probability at least $ 1 - \exp \big( -\frac{n \delta^2}{ 2 b^2 }\big)$. Consequently, as long as $\mathcal{R}_n(\mathcal{F}) = o(1),$ we have $\vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert _{\mathcal{F}} \overset{a.s.}{\rightarrow} 0 $.

proof)

• Borel-Cantelli lemma

Let $\epsilon >0$ and define

\[A_n (\epsilon) = \{ s \in S : \lvert X_n (s) - X(s) \rvert \geq \epsilon \}\]

Borel-Cantelli lemma says that if $\sum_{i=1}^\infty \mathbb{P}(A_n (\epsilon))< \infty, \quad then \quad X_n \overset{a.s.}{\rightarrow} X$

For above case,

\[\mathbb{P} (A_n ) = Prob (\lVert \mathbb{P} _n -\mathbb{P} \rVert_{\mathcal{F} } \geq 2 \mathcal{R}_n (\mathcal{F}) + \delta ) < \exp \bigg( -\frac{n \delta^2}{2b^2} \bigg)\]

Therefore, since $\sum_{n=1}^{\infty} \exp \bigg( - \frac{n \delta^2}{2b^2} \bigg)< \infty$, the Borel-Cantelli lemma guarantees $\lVert \mathbb{P} n -\mathbb{P} \rVert{\mathcal{F} } \overset{a.s.}{\rightarrow} 0$ from the statement. Accordingly, the remainder of the argument is devoted to proving the inequality,

\[\vert \vert \mathbb{P}_n - \mathbb{P} \vert \vert _{\mathcal{F}} \leq 2 \mathcal{R}_N (\mathcal{F}) + \delta\]

which will lead to uniform convergence of CDF .

• Step 1) concentration around mean

Let’s say that $\lVert \mathbb{P}_n - \mathbb{P} \rVert _{\mathcal{F}} := G(X_1 , \cdots , X_n)$. Then, to show the concentration around the mean, I will show the bounded difference condition of $G$ with $\max L_i \leq \frac{2b}{n}$.

\(\begin{align} & \quad\,\,\bigg\lvert \frac{1}{n} \sum_{i=1}^n{\bigg( G(X_1 , \cdots, X_n)} - \mathbb{E}\lbrack{G(X_1 , \cdots, X_n)}\rbrack\bigg) \bigg\rvert - \underset{G \in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n{\bigg( G(Y_1 , \cdots, Y_n)} - \mathbb{E}\lbrack{G(Y_1 , \cdots, Y_n)}\rbrack\bigg) \bigg\rvert\\ &\leq \bigg\lvert \frac{1}{n} \sum_{i=1}^n{\bigg( G(X_1 , \cdots, X_n)} - \mathbb{E}\lbrack{G(X_1 , \cdots, X_n)}\rbrack\bigg) \bigg\rvert - \bigg\lvert \frac{1}{n} \sum_{i=1}^n{\bigg( G(Y_1 , \cdots, Y_n)} - \mathbb{E}\lbrack{G(Y_1 , \cdots, Y_n)}\rbrack\bigg) \bigg\rvert \\ &\leq \frac{1}{n } \bigg\lvert \sum_{i=1}^n{\bigg( G(X_1 , \cdots, X_n)} - \mathbb{E}\lbrack{G(X_1 , \cdots, X_n)}\rbrack\bigg) - \sum_{i=1}^n{\bigg( G(Y_1 , \cdots, Y_n)} - \mathbb{E}\lbrack{G(Y_1 , \cdots, Y_n)}\rbrack\bigg) \bigg\rvert \\ & \leq \frac{2b}{n } \quad \longleftarrow b-uniformly\,\,\, bounded\\ &\longrightarrow\quad sup \,\,\,on\,\,\,each\,\,\,side\\ & G(X_1, \cdots, X_n) - G(Y_1 , \cdots, Y_n ) \leq \frac{2b}{n} \end{align}\)

Then, by McDiard’s theorem ,

\[\lVert \mathbb{P}_n - \mathbb{P} \rVert_{\mathcal{F} } - \mathbb{E} [\lVert \mathbb{P}_n - \mathbb{P} \rVert_{\mathcal{F} }] \leq t\]

with probability at least $1- exp (- \frac{nt^2}{2b^2 })$.

• Step 2) Upper bound on the mean

\[\begin{align} \mathbb{E} [\lVert \mathbb{P}_n - \mathbb{P} \rVert_{\mathcal{F} }] &\leq \mathbb{E}_{X} \bigg\lbrack \underset{f \in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n \lbrace f(X_i) - \mathbb{E}_{Y_i}[ f(Y_i)] \rbrace \bigg\rvert \bigg\rbrack \\ & = \mathbb{E}_{X} \bigg\lbrack \underset{f \in \mathcal{F}}{sup} \bigg\lvert \mathbb{E}_{Y_i} \big\lbrack \frac{1}{n} \sum_{i=1}^n \lbrace f(X_i) - f(Y_i) \rbrace \big\rbrack \bigg\rvert \bigg\rbrack \\ & \leq \mathbb{E}_{X,Y} \bigg\lbrack \underset{f \in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n \lbrace f(X_i) - f(Y_i) \rbrace \bigg\rvert \bigg\rbrack \\ &= \mathbb{E}_{X,Y,\epsilon} \bigg\lbrack \underset{f \in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n \epsilon_i \lbrace f(X_i) - f(Y_i) \rbrace \bigg\rvert \bigg\rbrack \\ & \leq 2\mathbb{E}_{X,Y,\epsilon} \bigg\lbrack \underset{f \in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n \epsilon_i \lbrace f(X_i)) \rbrace \bigg\rvert \bigg\rbrack \\ & = 2\mathcal{R}_n (\mathcal{F}) \end{align}\]

Combining results, one can get given inequality.

3. Upper bounds on the Rademacher complexity

3.1. Polynomical discrimination

Definition ( Polynomial Discrimination)

A class $\mathcal{F}$ of functions with domain $\mathcal{X}$ has polynomial discrimination of order $\nu \geq 1 $ if, for each positive integer $n$ and collection $x_1^n = \lbrace x_1 , \cdots, x_n \rbrace$, the set

\[\mathcal{F}(x_1^n) = \lbrace (f(x_1), \cdots, f(x_n) ) : f \in \mathcal{F} \rbrace\]

has cardinality upper bound as

\[card (\mathcal{F }(x_1^n)) \leq (n+1)^\nu\]

The significance of this property is that it provides with a straightforward approach to controlling the empirical Rademacher complexity

3.2. Bound on the empirical Rademacher complexity

Suppose that $\mathcal{F}$ has polynomial discrimination of order $\nu$. Then, for all positive integers $n$ and any collection of points $x_1^n = (x_1 , \cdots, x_),$

\[\mathbb{E}_\epsilon \bigg \lbrack \underset{f\in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n \epsilon_i f(x_i) \bigg\rvert \bigg\rbrack \leq 2 D(x_1^n) \sqrt \frac{v log(n+1)}{n}\]

, where $D(x_1^n) = \underset{f\in\mathcal{F}}{sup }\sqrt{\frac{1}{n} \sum_{i=1}^n f^2 (x_i) }$ is the $\mathcal{l}_2$ - radius of the set $\mathcal{F}(x_1^n)/\sqrt{n}$.

proof)

For any fixed vector $a = (a_1 , \cdots, a_n) \in \mathbb{R}^n$, the random variable $\frac{1}{n}\sum_{i=1}^n \epsilon_i a_i$ is sub-Gaussian with variance proxy $\sigma^2 = \frac{1}{n^2} \sum_{i=1}^n a_i^2$ . Since $\mathcal{F}$ has polynomial discrimination of order $\nu$, there are at most $(n+1)^\nu$ vectors of the form $(f(x_1) , \cdots , f(x_n))$, and each such vector has $l_2$- norm bounded by

\[\frac{1}{n}\sum_{i=1}^n f^2 (x_i) \leq D^2 (x_1^n )\]

Therfore, the empirical Rademamcher complexity is upper bounded by the expected supremum of $(n+1)^\nu$ Rademacher variables, each with variance proxy at most $D^2 (x_1^n) /n$. Applying maximal inequality of sub-Gaussian, it yields that

\[\begin{align} \mathbb{E}_\epsilon \bigg \lbrack \underset{f\in \mathcal{F}}{sup} \bigg\lvert \frac{1}{n} \sum_{i=1}^n \epsilon_i f(x_i) \bigg\rvert \bigg\rbrack & \leq D(x_1^n) \sqrt \frac{2 log(2(n+1)^\nu)}{n} \\ & \leq 2 D(x_1^n) \sqrt \frac{v log(n+1)}{n} \end{align}\]

---

• one of maximal inequality used here

Let $X_1 , \cdots , $ be zero-mean sub-Gaussian random variables with proxy $\sigma^2$

Then, $\mathbb{E} [ \underset{1\leq i \leq n} {max} \lvert X_i \rvert] \leq \sigma \sqrt{2 log (2n)}$

---

3.3. Glivenko-Cantelli theroem

Corlloary (Glivenko- Cantelli)

Let $F(t) = \mathbb{P} (X \leq t)$ be the CDF of a random variable $X$, and let $\hat{F}_n$ be the empirical CDF based on $n$ i.i.d. sample $X_i \sim \mathbb{P}$. Then, for all $\delta >0$ and $n \geq 1$,

\[\lVert F - \hat{F}_n \rVert_{\infty} \leq 4 \sqrt{ \frac {log (n+1)}{n}} + \delta\]

with probability at least $1 - \exp \bigg( - \frac{n \delta^2}{2b^2} \bigg)$. Therefor, $\lVert F - \hat{F}_n \rVert _\infty \overset{a.s.}{\rightarrow} 0$

proof )

Because for a givne sample $x_1^n = (x_1 , \cdots ,x_n) $ and function class $\mathcal{F} = \lbrace I_{(-\infty , t \rbrack} (\cdot) : t \in \mathbb{R} \rbrace $, consider the set $\mathcal{F}(x_1^n ) = \lbrace f(x_1) , \cdots , f(x_n) : f \in \mathcal{F} \rbrace$. Because it only divides real line into $n+1$ parts, cardinality is $n+1$, which means that polynomial discrimination of order 1. Then, by the results above, given inequalities works.

3.4. Vapnik-Chervonenkis dimension

Above, we see that Polinomical discrimination is useful to find the upper bound. One of way to verify that a given function class has polynomial discrimination is via the thoery of VC dimension. Consider a function class $\mathcal{F}$ where each function $f$ is binary-valued, {0,1} for simplicity. Then the set $\mathcal{F} (x_1^n)$ has at most $2^n $ elements. (Of course, because each element has 2 possibilities).

Definition (VC dimension) Given a class $\mathcal{F}$ of binary-valued functions, we say that the set $x_1^n = (x_1 , \cdots, x_n)$ is shattered by $ \mathcal{F}$ if card($\mathcal{F}(x_1^n)) = 2^n$. The VC dimension $\gamma(F)$ is the $largest$ interger $n$ of which there is some collection $x_1^n = (x_1, \cdots ,x_n )$ of $n$ points that is shatter by $\mathcal{F}$.

• Example : Two-sided Intervals in $\mathbb{R}$

Consider the collection of all two-sided intervals over the real line – namely $\mathcal{S_{both}} = { (b,a \rbrack : a,b \in \mathbb \,\,\, such \,\,\,that \,\,\, b < a }$. The class $\mathcal{S} _ {both}$ can shatter any two distinct points. However, given three distinct points $x_1 < x_2 < x_3$, it is not possible to pick out the subset {$x_1, x_3$}, showing that the VC dimension $\nu (\mathcal{S}_{both}) = 2$.

• Sauer’s Lemma

Consider a set class $\mathcal{F}$ with the VC dimension $\gamma{(\mathcal{F}) < \infty}$. Then, for any $n > \gamma({\mathcal{F}})$, we have that

\(card (\mathcal{F} (x_1^n)) \leq (n+1)^{\gamma (\mathcal{F})}\)

3.5. Multivariate version of Glivenko-Cantelli

Theorem

Let $X_1, \cdots , X_n$ be $i.i.d.$ obesrvations frnom a distribution $P $ on $\mathbb{R}^d$ . let $F$ denot the multivariate cumulative distribution function of $P$, that is

\[F(\bf{x}) = \mathbb{P} (\bf{X \leq \bf{x}}), \quad \bf{x} \in \mathbb{R}^d\]

where for vectores $\bf{x} = (x_1, \cdots, x_d)$ and $\bf{y} = (y_1, \cdots, y_d)$ in $\mathbb{R}^d $ , $\bf{x} \leq \bf{y}$ means that $x_j \leq y_u$ for all $j=1, \cdots, d$. Let $\hat{F}_n$ denote the empirical CDF of $P$, i.e.

\[\hat{F}(\bf{x}) = \frac{1}{n} \sum_{i=1}^n I(\bf{X}_i \leq \bf{x}), \quad \bf{x} \in \mathbb{R}^d\]

Then,

\[\vert \vert \hat{F} (\mathbf{x}) - F(\mathbf{x}) \vert \vert _\mathcal{\infty} \leq 2 \mathcal{R}_n (\mathcal{F}) + \delta \leq 4 \sqrt{\frac{d log(n+1)}{n}} + \delta\]

, with probability at least $1- exp(- \frac{n \delta^2 }{2})$.

proof)

At first, class of indicator functions characterized by the class of sets $\mathcal{A} = { (-\infty , x_1] (-\infty , x_2]\times (-\infty , x_d],(x_1, \cdots, x_d \in \mathbb{R}^d)}$ has VC dimension $d$.

because $\mathcal{A}$ has VC-dimension $d$, apllying sauer’s lemma, for fixed $x_1^n$ , we haver

\[card(\mathcal{F} (X_1^n)) \leq (n+1)^d\]

, which means that $\mathcal{F}$ has polynomical discrimination of order $d$.

Because class $\mathcal{F}$ is 1-uniformly bounded (Because it is CDF), implement Glivenko-Cantelli property, for any positive interger $n \geq 1$ and any scale $ \delta \geq 0 $, we have

\[\vert \vert \hat{F} (\mathbf{x}) - F(\mathbf{x}) \vert \vert _\mathcal{\infty} \leq 2 \mathcal{R}_n (\mathcal{F}) + \delta \leq 4 \sqrt{\frac{d log(n+1)}{n}} + \delta\]

with probability at least $1- exp(- \frac{n \delta^2 }{2})$, which is,

\[\mathbb{P} \bigg( \vert \vert F-\hat{F}_n \vert \vert_{\infty }\geq 4 \sqrt{\frac{d log(n+1)}{n}} + \delta \bigg) \leq exp(- \frac{n \delta^2 }{2})\]