In progress

A Unified Approach to Interpreting Model Predictions

Date :     Updated :

1. introduction

  1. The SHAP value is the unified approach for any explanation of a model’s prediction as a model itself.

  2. Game theory results guarantee that a unique solution apply to the entire class of additive feature attribution methods and SHAP value is the measure for the unique solution

  3. Author proposes that SHAP is fit well with human intuition

2. Additive Feature Attribtuion Methods

machine Learning model is so complex ; it itself cannot explain its results.

Instead, we can use simpler explanation model to approximately explain the result of the original model. The simplest model is additive model.

Let say $f$ is original model and g is explanation model for it.

Definition. Additive Feature Attribution methods have an explanation model that is a linear function of binary variables: \(g(z') = \phi _0 + \sum _{i=1} ^{M} \phi_i z_i'\) here, $z’ \in {0,1}^M$ , $M$ is the number of simpilifIed input features, and $\phi_i \in R$

here, $z’$ is simplified variables for the original variables.

Definition.

Additive Feature Attribution methods have an explanation model that is a linear function of binary variables: \(g(z') = \phi _0 + \sum _{i=1} ^{M} \phi_i z_i'\) —

here, $z’ \in {0,1}^M$ , $M$ is the number of simpilifIed input features, and $\phi_i \in R$


여기서, $z’$ 은 simplified variables for the original variables.

만일 실젯값이 $f(x)$ 라면, $g(z’) = f(h(z’)) = f(x)$ .

LIME

  • LIME은 대표적인 Additive Feature Attribution method 중 하나. 모델에 의해 어떤 예측값이 주어졌을 때, 해당 예측값에서의 국소적인 선형 모델을 근사한다.

  • LIME은 위의 Definition에 일치하는 해석을 가진다. 어떤 예측값 $g(z’)$가 주어졌을 때, 독립변수 $x$ 값들을 1과 0의 $binary ~~ variable ~~z$’ 로 전환한다. 그리고 각각의 예측값에 대해 $h(z’) = x$를 만족하는 $h$를 만들어낸다.


  • LIME의 목적함수는 다음과 같음.
\[\min\limits_{g \in G } L( f , g, \pi _{x'}) + \Omega (g) \\\]
  • \[\\ one ~example~ : ~ L (f,g, \pi_x ) = \sum\limits_{z , z' \in Z}\pi_x(z) (f(z) - g(z'))^2\]


  • 이때, $z$ 는 관측치를 설명하고자 만드는 이웃데이터들이다. LIME이란게 어떤 local point의 인근에 있는 관측치들을 바탕으로 국소적인 모델을 만드는 것. 예를 들어, 아래의 그림에서 $x$가 실제 데이터이고, $z$는 해당 데이터 근처에서 값들을 살짝씩 바꿔 만든 추가적인 이웃데이터이다.


  • $z’$ 은 $z$ 보다 낮은 차원의 데이터로 ,복잡한 모델을 간단하게 설명하기 위해 차원을 줄이는 것. 예를 들자면, LASSO 방법론을 통해 들어오는 input data $z$를 차원이 적은 $z’$으로 줄이기도 합니다.

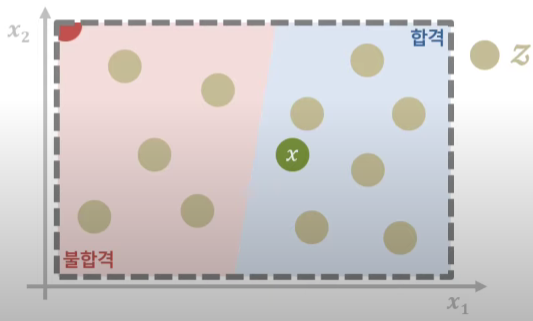
image-20220805004943561

출처 : 김성범 인공지능 연구소


  • $f$ 는 우리가 해석하고자 하는 본래의 복잡한 모델, $g$는 해석을 위한 간단한 모델, $\pi_{x’}$은 $z$와 $x$ 사이의 거리에 의해 부여된 가중치. 즉, 실제 $x$에 가까운 $z$일 수록 해당 $x$ 가 모델에서 가지는 의미를 잘 설명할 것이므로, 가까울 수록 더 높은 가중치를 부여함.

image-20220805021514461

출처: Local interpretable model-agnostic explanations (lime), 2016.


  • 라임을 설명하는 대표적인 그림은 위의 이미지. 예를 들어, 32x32x3 이미지가 있다고 했을 때 ($R^{3072} $)

    $x = (0.12, 0.23, …. , 0.88)$과 같은 32x32x3의 dim vector로 이미지가 나타날 것이다.

    이를 (0,1,0, … ,1, 0)의 $M$ dim $z’$로 간단하게 표시하는데, 이것이 위에서 오른쪽 그래프와 같이 사진을 잘게잘게 쪼개놓은 부분.

image-20220805022119791


  • 즉, 어떤 데이터를 (0,1)의 binary variable로 축약하여 표현하고($z’$) 이들 근처의 이웃데이터들에 대해 국소적 모형을 정의하여 개별 데이터를 설명한다.



Classic Shapley Value Estimation

  • Shapley Value는 협조적 게임이론에서 나온 이론으로, 어떤 player가 게임에서 빠지면 결과가 얼마나 바뀌는지를 계산함으로써 player의 기여도를 계산하는 방식.


  • 간단한 3인 게임 Shapley value 계산의 예는 다음과 같음.

  경기자 1 경기자 2 경기자 3 점수
1 o o o 30
2 o o x 27
3 o x o 24
4 x o o 25
5 o x x 14
6 x o x 13
7 x x o 10
8 x x x 0


  • 경기자 1의 Shapley value

    경기자 1이 빠질 수 있는 경우의 수를 모두 더하면 됨.

    1. 1 –> 4 : 기여도 =5

    2. 2 –>6 : 기여도 = 14

    3. 3–> 7 : 기여도 = 14

    4. 5 –> 8 : 기여도 = 14

    이에 대한 가중평균을 하면 흔히 구하는 shapley valuer가 계산된다.

    (가중치는 1은 1/3, 2는 1/6, 3은 1/6, 4는 1/3)


  • 이에 대한 일반화 식은 다음과 같음.

\[\phi _i = \sum_{S \in F / \{ i\}} \frac{|S|! (|F| - |S| -1)!}{|F|!} [f_{S \cup \{i\} } (x_{S \cup \{ i \}}) - f_S (x_S )]\]

이런 shapley value의 계산은 위의 예시에서 보듯 있으면 1, 없으면 0 과 같은 방식으로 이해할 수 있기 때문에, additive feature attirubtion method라고 할 수 있음.


  • 위의 가중평균 기여도는 다음과 같다. 경기자가 3명이므로 $F$ = {1,2,3}

    위의 예시와 같이 경기자 1을 기준으로 생각할 때, $S$가 가질 수 있는 $F/ { 1 }$ 의 부분집합은 $\phi$ , {2}, {3}, {2,3}

    $\phi$ : 5->8. 기여도 = $\frac{1! (3 - 0 -1)!}{3!} = \frac{1}{3}$

    {2} : 2->6. 기여도 = $\frac{1! (3 - 1 -1)!}{3!} = \frac{1}{6}$ {3} : 3->7. 기여도 = $\frac{1! (3 - 1 -1)!}{3!} = \frac{1}{6}$ {2,3} : 1->4. 기여도 = $\frac{2! (3 - 2 -1)!}{3!} = \frac{1}{3}$



3. Simple Properties Uniquely Determine Additively Feature Attribution

  • 저자에 의하면, Additively Feature Attribution methods 들 중에서,

    1. Local Accuracy
    2. Missingness
    3. Consistency

    의 3가지 성질을 만족하는 solution은 단 한개 존재하며, 그게 Shapley Value.

    이는 곧, LIME 등 shapley value가 아닌 다른 additive model은 위의 3가지 성질을 동시에 만족하지는 못한다는 것.


  1. Local Accuracy

    \[f(x) = g(x') = \phi_0 + \sum _{i=1}^{M} \phi _i x_i'\]

    가 성립할 때, 설명 모델 $g(x’)$ 는 기존 모델인 $f(x)$와 locally 일치한다.


  1. Missingness

    \[x_i'=0 ~~\rightarrow ~~\phi_0\]

    simplified feature가 0일 때 (<-> 어떤 feature가 없을 때) 해당 feature는 아무런 기여도 하지 못한다.


  1. Consistency

    Let $f_x(z’) = f(h_x(z’))$ and $z’/i$ denote setting $z_i’ =0$ , For any two models $f $ and $f’$ , if

    \[f_x'(z') - f_x'(z'/i) ~ \geq~f_x (z') - f_x (z'/i)\]

    for all inputs $z’ \in { 0,1 }^M$, which means that $\phi_i(f’,x) \geq \phi_i (f,x)$

    즉, 어떤 변수의 변동으로 인한 종속변수의 변동이 커지면, 그에 상응하는 방향으로 feature attirubution도 증가하거나 감소한다.

Theorem 1

Only one possible explanation model $g$ follows definition of additive feature attirbution model satisfying properties 1,2,3 :


\(\phi_i (f,x) = \sum_{z' \in x'} \frac{|z'|! (M-|z'| -1)!}{M!} [f_x (z') - f_x (z'/o)]\)

where $ z’ $ is the number of non-zero entries in $z’$ and $z’ \in x’$ represents all $z’$ vectors where the non-zero entries are a subset of the non-zero entries in $x’$


Theorem 1은 과거 경제학자들에 의해 증명되었으며, 이는 Shapley value를 의미한다.


4.SHAP values

  • Lundberg는 본래 모델에 대한 조건부 평균의 shapley value를 SHAP value로 정의한다 :


    \(f_x (z') = f(h_x (z')) = E[f(x)|z_S]\)

    $S$ 는 binary에서 1로 설정된 $z’$ 의 집합을 의미.


  • 이런 과정을 그림으로 나타내면 아래와 같다.


image-20220815190147039

feature가 하나도 안쓰일 때에는 $\phi _0$, $x_1$ 하나가 쓰인 순간 그 조건부평균을 넣어서 $\phi_1$ , …. 반복한다.


Kernel SHAP ( Linear LIME + Shapley Values)

  • 앞서 3장의 내용에서 얻을 수 있는 결론은, 기존에 사용되는 LIME 방법론은 3가지 property를 만족한다는 보장이 없다는 것이다.


  • 앞서 설명한 LIME의 최적화 식,
    \(\min\limits_{g \in G } L( f , g, \pi _{x'}) + \Omega (g) \\\)

    은 SHAP 과 다르게 보이지만, 위 식의 $L, \pi_x , \Omega(g)$ 를 조절하여 SHAP과 동일한 값을 얻을 수 있다는 것을 저자는 보였다. 이게 많이 사용되는 Kernal SHAP

Theorem (Shapley Kernel)

Under Definition 1, the specific forms of $\pi_x’$ $L$, and $\Omega$ that make solutions of above equation consistnt with properties 1,2,3 are :


\(\Omega(g) = 0\)
\(\pi_{x'} (z') = \frac{M-1}{(M choose |z'|)|z'| (M-|z'|)}\)
\(L(f,g, \pi_{x'}) = \sum_{z' \in Z} [f(h_x^{-1}(z'))-g(z')]^2 \pi_{x'} (z')\)

where $ z’ $ is the number fo non-zero elements in $z’$

##


5. Conclusion

  1. Computational Efficiency
    • Kernal SHAP은 model agnostic한 Shapley Value의 근사치로 Shapley Value에 비해 계산량이 확실히 적음.
  2. Consistency with Human Intuition
    • SHAP은 consistency가 성립하는 만큼, 우리의 일반적인 intuition과 일치하는 모습을 보이는 경우가 많음.
    • LIME, DeepLIFT 등 기존 XAI 방법론보다 직관적인 결과가 도출.
  3. Explaining Class Differences

(오류로 날라감. 추후에 복구)

첫 번째 글입니다 가장 최근 글입니다

Leave a comment

최근 글 10 개 :)